Reverse Engineering the Ansys TDM

My idea on how the Ansys TDM probably works

Recently, the software company Ansys released a new update with something extremely interesting. With something called time decomposition method, they claimed to be able to speed up time-stepping simulations by a factor of ten. And that was in 3D, and their white paper promised speed-ups up to 60x.

Needless to say, my interest was more than piqued.

I mean, I often get speed-ups of 60-100 in my work – and that’s research-focused and highly experimental. Software companies often tend to take the safer and slower route.

In that context, this TDM thing seemed quite amazing indeed.

Forgotten. But only for a moment.

Nevertheless, I only skimmed through the promotional material and continued with my day job. Gotta pay the bills and so on.

Business went on as usual until a colleague of mine (who’s by the way behind the free MotorAnalysis software – I gotta review that in the near future) brought it back to my attention and asked for input.

So, I turned my attention back to TDM.

Not my First Rodeo

Luckily, I had plenty of experience in reverse engineering. During the first two years of my Bachelor’s studies, I took four some freaking nightmarish kinda difficult courses on mathematics. Four two-hour lectures each week at 8 am sharp. Each worth a mental Cooper’s test, where a second’s lapse in concentration meant losing track completely.

Reverse engineering, also called back engineering, is the processes of extracting knowledge or design information from anything man-made and re-producing it or re-producing anything based on the extracted information. –Wikipedia

And they were accompanied by home assignments. Which, in our opinion, meant that you went home with the assignments, broke your figurative spine on them, and came back the next day for more. At least that was all you had time for.

Why We Reverse-Engineered

Our savior was the university license to Wolfram Mathematica. For those who don’t know, Mathematica is a freaking amazing symbolic calculation software (Wolfram corporation please pay me now). Check out Wolfram Alpha, and then realize the proprietary software version was 20 times better even back in 2008. Yup, that good.

Anyway, Mathematica saved our academic lives. It couldn’t solve any advanced tasks for us (“Prove the existence and uniqueness of-“), but it could evaluate difficult integrals, among other things. We would feed Mathematica the integrand, and it would spit out the closed-form indefinite integral.

But that wasn’t of course enough to get any points at all from the assignment. For that purpose, you had to show them that you understand how the expression was derived.

So that’s how it went. We’d go home, get the expression out from Wolfram’s Magic Box, and then spend the next day (or three, plus some nights) figuring out how you arrive at that.

Reverse engineering.

Now multiply that by four semesters.

Reverse Engineering the TDM

With these reserves of experience to draw on, I set to reverse engineering the Ansys TDM.

Of course, I was slightly hindered by the fact that I didn’t even have access to the software itself let alone source codes. So take what I have to say with a colossal grain of salt.

What we Know

Let’s start with the easiest snippet of information. The TDM is an HPC algorithm – meaning high-performance computing. Typically meaning large-scale parallel computing, be it with supercomputers or clusters.

So, the algorithm utilizes massive computing power to ramp up the speed, rather than getting more with the same power like I do.

Note that I’m not scolding Ansys now – far from it. It’s no easy feat to develop algorithms that can be executed in parallel.

What we also Know

Ansys is kind enough to provide another piece of information. They state that all (or at least several) time steps are solved simultaneously. Now this might actually get us somewhere.

If you haven’t yet checked out some basics of time-stepping analysis, do it now. Otherwise, the following may be hard to understand.

In the simplest form of time-stepping FEM, the unknown vector at time-step is solved with the Backward Euler method from the equation

.

As can be seen, the time-step is coupled to the previous one through the mass matrix .

What Probably Happens under the Hood

Now, we want to solve all steps at the same time. While that may seem difficult due to the aforementioned coupling between the time-steps – in principle it is not. We can simply write a huge block matrix equation for all the time-steps together.

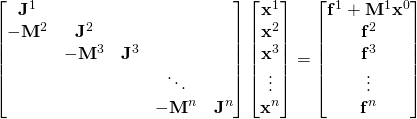
As you can see, the dependency between the time-steps is now almost fully included in the left-hand-side matrix. The only exception is the ininitial condition , which is considered in the first block of the load vector.

Steady-State Delivered to your Doorstep

This type of simultaneous solution method has one attractive feature. Very often, we desire the steady-state behavior of an electrical machine. That means the behavior of the machine – currents, torque, everything – stays identical from one period of the supply voltage to another. However, to actually get even near that state, several hundred time-steps are often needed.

Not so with this method of analysis. Remember the initial condition ? Well, in steady-state we have by definition

.

In other words, the initial conditions must match the end state of the problem. In time-stepping analysis this helps us precisely frak-all, since we don’t know the final state beforehand. However, when we are solving all time-steps at the same time, we can just-as easily include this periodicity condition in the system matrix like this:

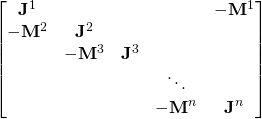
To point out the difference: look at the upper-right corner of the matrix. The condition is now included there, by the mass matrix multiplying the final time-step value.

So there we have the very basics. Time-stepping analysis doesn’t in principle need stepping as commonly understood, i.e. a succession of steps. Nope, we can combine them into a single step, with the additional benefit of easy steady-state analysis.

Simple as that.

What Might be Happening under the Hood

Well, it’s not. The principle still stands. But, as I mentioned, the matrix will indeed be HUGE. Even in 2-dimensional analysis, and even more so in 3D.

You see, most problems in 2D, and simple ones in 3D, can be solved by a direct method. That means Gaussian elimination in principle, and some kind of sparse-matrix specific frontal solver in practice (Matlab uses UMFPACK). Direct methods are quite fast nowadays, and even more importantly they’re robust. You give the matrix, you get the solution. Simple as that.

But, they cannot be used for problems this big. Instead, some kind of an iterative method is needed. Most often, we use some Krylov subspace method, like the conjugate gradient or GMRES. Unlike direct methods, iterative ones don’t even require the matrix to actually exist in matrix form – they only want to be able to multiply a vector by it.

Hence, they are at least much more forgiving with RAM requirements, if not downright faster. Unfortunately, they almost never work as such, at least not in electromagnetics. Instead, they need some kind of preconditioner.

A Pre-What?

A preconditioner is something – it can be a matrix, or some piece of program or algorithm – that approximates the solution to our problem. And does it much faster than actually solving our problem, of course. It wouldn’t make any sense otherwise.

In our case (and in maaaany other cases, for that matter), a possible first candidate for a preconditioner is

In other works, we take the block-diagonal parts of our system matrix. That’s still a huge matrix, but now you see we can solve each part

independently of the others. (Note:  is simply something that the Krylov method feeds to the preconditioner. No need to concern ourselves with that yet.)

Thus, the preconditioner can easily run in parallel.

But of course, that’s only one option. We can also run several cycles of the preconditioner while updating the -matrix contribution to the right-hand-side. In this case, we end up with something close to the additive Schwarz method – a well-known domain-decomposition method.

Or, we can eliminate all step-specific variables from the problem, leaving us only with the currents plus the conductor nodes to solve. This would correspond to an iterative substructuring method. Or maybe some kind of waveform relaxation, if we drop some dependencies.

There are lots of options.

Once more, with Feeling

One more thing springs to mind. The above approach works better if we start it quite close to the problem solution. Luckily, that is not very hard to do with electrical machines.

We understand them quite well, so we can draw on that knowledge base.

For instance, if steady-state analysis interests us, we can begin with harmonic analysis. In other words, we assume a purely sinusoidal behavior and use that as our initial state. With most machines, that actually hits quite close.

Or, if start-up characteristics interest us, we can first do a single simulation to determine the equivalent circuit parameters of the machine. Using those, we determine a rough torque-speed curve and use that to initialize our simulation.

Or, use a multigrid method in time – do a few steps of normal time-stepping with the largest step we can manage.

Or, one some combination of the above.

Or, some other of the million tricks we engineers have a habit of thinking up.

Disclaimer

I’d like to emphasize that almost all of the above – everything not explicitly stated by Ansys – is purely hypothetical. I have no idea if the TDM really works like that. It might be something else altogether.

But, it’s still my best guess, right now, on how to do it. It’s simple, and all the best algorithms are.

And it’s ugly, too – there’s probably a smarter and faster way to do things. But ask anybody in the software industry about horrible temporary workarounds becoming horrible permanent workarounds. My approach won’t seem too ugly after all.

Waving-contest time

Finally, you remember my work on speeding up time-domain analysis with the harmonic balance method. How does that compare to the Ansys TDM?

Well, they approach the problem from different angles.

Ansys adopts the pure-HPC route. Heavy computing, with all steps explicitly solved. Highly parallelizable.

Harmonic balance FEM casts the time-dependency into the Fourier-space. It often reduces the size of the total problem a lot but does it at a cost of denser system. Meaning it takes longer to solve, and is not as easy to run in parallel.

And they both work. But, I would bet the former is more suitable for actual supercomputers, while the latter is probably more beneficial on typical current workstations.

That was all today. Easily the longest post I have ever written.

What’s your opinion on this topic – let me know in the comments!

-Antti

Reverse Engineering the Ansys TDM